Геометрия, 7 класс.

Пифагор, наверное, любил играть в пятнашки. Помните такую игру? В квадратной коробочке нужно передвигать маленькие квадратики с числами. Сделайте «пятнашки» из четырех одинаковых прямоугольных треугольников разного цвета, которые можно свободно перемещать в квадратной коробочке. Получится наглядное пособие для демонстрации теоремы Пифагора, а также для тренировки воображения.

Математические образы – это схемы, графики, геометрические фигуры. Чтобы запоминать математические понятия, нужно тренировать свое воображение манипулировать математическими образами.

Рис. 1	Рис. 2

На (рис.1) исходное положение треугольников. Четыре треугольника образуют черный квадрат в центре. Смещайте пальцем желтый треугольник в сторону голубого треугольника. А красный и зеленый – в нижний правый угол (рис. 2). В результате перестановки треугольников площадь черного квадрата распределилась между площадями двух других черных квадратов, меньших по размеру.

Такие перестановки треугольников нужно уметь делать в своем воображении, с помощью визуального мышления. Представьте исходное положение треугольников (рис. 1). Мысленно переместите желтый треугольник. Мысленно переместите красный и зеленый треугольники. Представьте конечное положение треугольников (рис. 2).

Визуальное мышление должно заменить запоминание формул. Действительно, зачем их запоминать, если вся необходимая информация содержится в иллюстрации? Вместо запоминания доказательства запоминаем простые картинки. И по картинкам, как по шпаргалке, читаем формулы.

В математике все взаимосвязано. Фактически, нужно знать только формулу площади прямоугольника, чтобы вывести все остальное, необходимое для понимания и доказательства теоремы Пифагора.

Формула площади треугольника «читается» по картинке прямоугольника (рис. 3). Площадь треугольника равна половине площади прямоугольника.

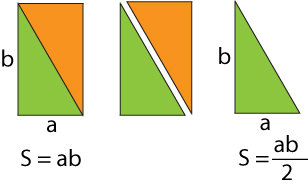
Рис. 3

Из четырех одинаковых прямоугольных треугольников составляем большой квадрат (рис. 4), в центре которого также получается квадрат. По картинке видно, что площадь сине-зеленого квадрата равна ( a + b)^2. Ведь сторона квадрата образована двумя катетами разных треугольников, a и b.

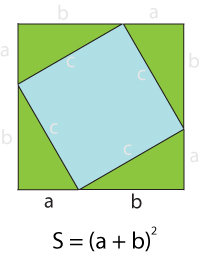
Рис. 4

Площадь фигуры (рис. 5), образованной четырьмя треугольниками (без внутреннего квадрата), равна площади одного треугольника умноженного на четыре. Двойка сокращается, и площадь четырех треугольников получается равной 2ab.

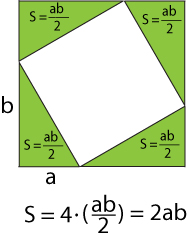
Рис. 5

Площадь внутреннего (голубого) квадрата (рис. 6), равна c^2.

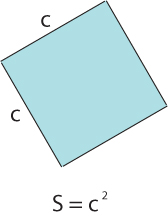
Рис. 6

Назовем фигуру на (рис.4) - большим квадратом. На (рис. 5) – треугольники. На (рис. 6) – маленький квадрат.

Чтобы запомнить доказательство, нужно представить равенство в виде зрительных образов, как на (рис. 7).

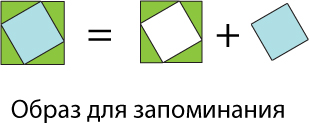
Рис. 7

Площадь большого квадрата равна сумме площадей треугольников и маленького квадрата.

Теперь, удерживая в воображении равенство, составленное из трех картинок, считывайте с картинок буквы и переводите равенство на математический язык. Мысленно пишите формулы в своем воображении.

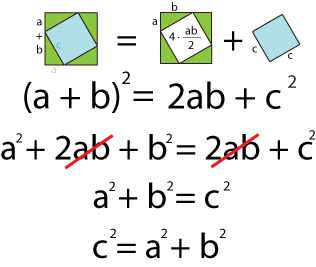
Рис. 8

Вспоминаете большой квадрат – мысленно напишите, чему равна его площадь. Она равна ( a + b)^2.

Представьте фигуру, образованную треугольниками. Мысленно напишите в воображении формулу площади этой фигуры. 4 х ( ab/2), двойка сокращается, получается 2ab.

Представьте внутренний квадрат. Мысленно напишите формулу его площади. Площадь равняется c^2.

Используйте свой «зрительный блокнот», чтобы рисовать геометрические фигуры и писать формулы.

Разложите квадрат суммы. Мысленно напишите а^2 + 2ab + b^2. Продолжайте мысленно писать равенство… равняется 2ab + c^2.

Формулы запоминать не нужно! В вашем воображении (в вашей памяти) есть равенство из трех геометрических фигур (рис. 7), с которых вы и читаете нужные вам формулы.

Сократите 2ab в левой и правой частях равенства. Теорема доказана.

Теорема в учебниках формулируется так: квадрат гипотенузы равен сумме квадратов катетов.

Однако, для лучшего понимания сути, можно дать буквальную (наглядную) формулировку (рис. 9). Площадь квадрата построенного на стороне (c) равна сумме площадей квадратов построенных на сторонах (a) и (b) прямоугольного треугольника. То есть, стороны прямоугольного треугольника связаны через площади квадратов, построенных на соответствующих сторонах треугольника.

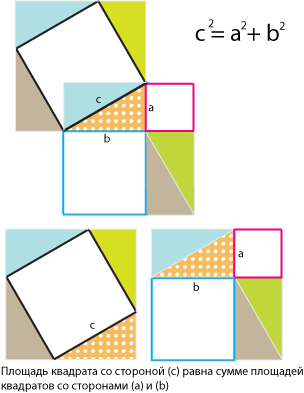
Рис. 9

Когда вы смотрите на формулу c^2 = a^2 + b^2, воображение должно подставлять картинку, как на (рис. 9). За словом «квадрат» (и за обозначением квадрата) нужно видеть геометрический квадрат, а не произведение двух букв.

Итак, мы убедились, что при запоминании теоремы Пифагора и её доказательства, запоминать, на самом деле, нечего! Единственное что нужно запомнить – это картинку на (рис. 7). С этой картинки легко считывается вся необходимая информация. Фактически из мнемотехники используется только навык визуализации.

Можно дополнительно запомнить на картинку (рис. 7) номер параграфа и номер страницы в учебнике, с помощью образных кодов чисел.

В.Козаренко

Дата размещения материала на сайте: 8 декабря 2011 года