Визуализация синуса

Запоминание через понимание

Смотрим определение синуса в учебнике геометрии. "Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе".

Дает ли это определение понимание синуса? Нет, не дает. Определение не полное. Потому что оно рассматривает только частный случай треугольника - прямоугольный треугольник.

Смотрим определение синуса в учебнике алгебры. "Ордината точки Р, полученной при повороте точки Р (1;0) вокруг начала координат на угол а-радиан, называется синусом числа а, а абсцисса этой точки - косинусом".

Это определение вообще из области математической абстракции, так как вводит отрицательные значения синуса и косинуса. И с пониманием синуса по этому определению ещё больше сложностей.

Есть простой тест на понимание синуса и косинуса. Попросите школьника нарисовать линию косинуса для произвольного треугольника (не прямоугольного). Если он этого сделать не может - он не понимает, что такое синус и косинус.

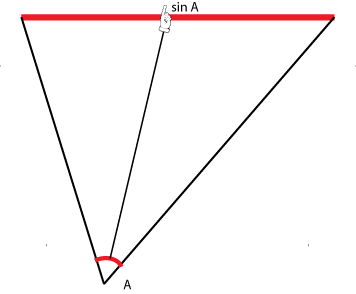
Иллюстрация 1. Тест на понимание. Где линия косинуса?
(Предполагается описанная окружность с единичным диаметром)

Итак, школьные учебники не дают информации для понимания понятий "синус" и "косинус". Основное понятие тригонометрии (и элементарное понятие) "засекретили", спрятали в частных случаях и в математических абстракциях.

При возникновении проблем с пониманием сейчас можно обратиться к поисковым системам и найти в них недостающую информацию. Чтобы визуализировать синус и косинус, нужно вернуться к истокам тригонометрии, понять, откуда эти понятия появились, и для каких целей.

Изначально синус не связан с треугольником. Синус появился из окружности и вписанного в окружность угла.

В окружности с единичным диаметром синус - это хорда, на которую опирается вписанный угол. А косинус - это перпендикулярная хорде-синусу хорда. На иллюстрации видно, что для любого вписанного угла в окружности имеется две линии синуса и две линии косинуса, которые образуют прямоугольник.

Вот эту иллюстрацию и следует использовать для запоминания понятий "синус" и "косинус". По этой иллюстрации можно дать определение синусу своими словами.

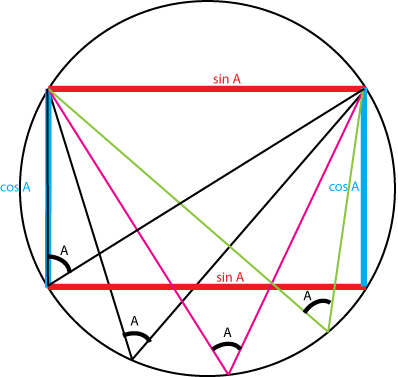
Иллюстрация 2. В окружности с единичным диаметром линии синуса и косинуса (для вписанного угла)
образуют прямоугольник. На картинке виден частный случай - прямоугольный треугольник,
в котором линия косинуса совпадает с катетом.

Связан ли синус (длина хорды) с противолежащим углом? Ведь мы привыкли говорить "синус угла". Связь длины хорды с углом очень не простая... Скорее, можно говорить о табличном соответствии длины хорды и величины вписанного в окружность угла.

Синус напрямую связан с другим элементом в окружности - с её диаметром. Если мы рассмотрим окружность с произвольным диаметром и вписанный в эту окружность произвольный треугольник (не прямоугольный), то синус получается путем деления стороны треугольника на диаметр этой окружности. То есть, синус - это коэффициент пропорциональности стороны вписанного в окружность треугольника. Понятие "синус" напрямую связано со стороной треугольника. Но традиции есть традции - принято говорить "синус угла".

Как получаются синусы сторон треугольника видно на иллюстрации ниже. Мы можем вычислить синусы всех сторон (или синусы всех углов, как принято говорить), измерив точной линейкой стороны треугольника и диаметр описанной окружности, и разделив каждую сторону на диаметр. Величины углов нам для этого не нужны.

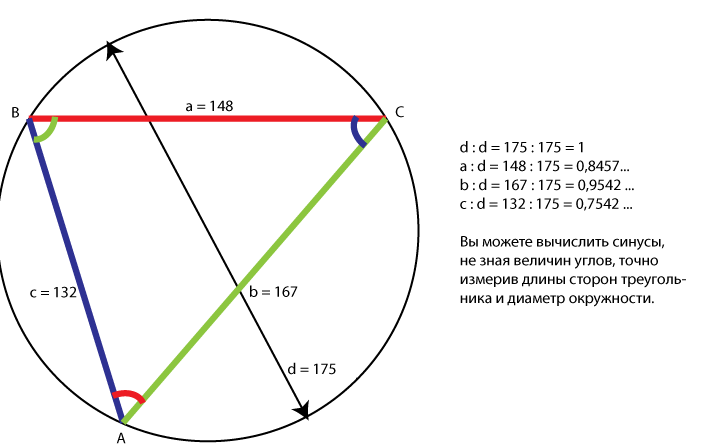
Иллюстрация 3. Опишем вокруг треугольника окружность
и точно измерим стороны треугольника и диаметр окружности

В результате мы получим пропорционально уменьшенный треугольник, вписанный в окружность с единичным диаметром, стороны которого и будут синусами сторон исходного треугольника.

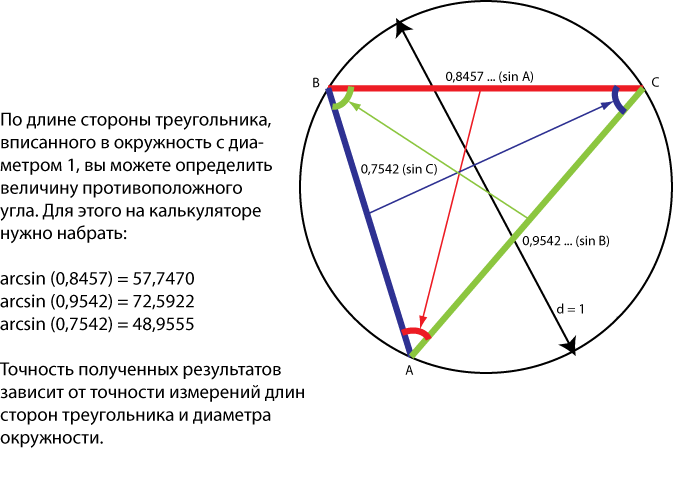
Иллюстрация 4. Стороны треугольника стали синусами,
когда мы уменьшили окружность до единичного диаметра

Усвоив понятие синуса, визуализировав его у себя в воображении, поняв, откуда оно появилось, можно переходить к частным случаям синуса и косинуса, изложенным в учебниках. Легко заметить, что в прямоугольном треугольнике одна из сторон (гипотенуза) одновременно является и диаметром описанной окружности. Теперь становится более понятным определение из учебника геометрии, по которому синус угла - это отношение катета к гипотенузе (т.е., к диаметру окружности). На иллюстрации 2 видно, что косинус совпадает со стороной треугольника только в прямоугольном треугольнике. В любом другом треугольнике линия косинуса находится вне треугольника. В учебнике алгебры, где синус рассматриваются как проекция точки окружности на ось координат, переходят на половины углов и полухорды, и с единичного диаметра на единичный радиус. Для чего? Чтобы ввести отрицательные значения тригонометрических функций.

На иллюстрации 3 и 4 видна теорема синусов. Теорема синусов является очевидной и не нуждается в доказательстве. Если синусы сторон (углов) изначально получены нами путем деления каждой стороны треугольника на диаметр описанной окружности, то отношение любой стороны треугольника к синусу стороны (синусу угла) будет одной и той же величиной, равной диаметру окружности. Это и есть теорема синусов.

a/sinA = b/sinB = c/sinC = d

(sin A - коэффициент пропорциональности стороны "a")

-------------------------------------------------

А как же все таки угол связан со своим синусом?

Ведь для решения задач удобно находить синус угла по значению самого угла. Сейчас это не проблема. На любом калькуляторе вы можете набрать sin (вставить угол) и получить результат с заданной точностью.

Изменение значения синуса при равномерном изменении величины угла визуально похоже на перемещение с равноускоренным движением (представьте падающий на землю шарик и его ускорение в каждую секунду). И очень приблизительные значения синуса (по углу) можно вычислить по формуле перемещения с равноускоренным движением. Но четкой функциональной зависимости значения синуса от величины угла нет. С заданной точностью синус вычисляется по формуле:

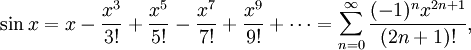
В.Козаренко

Дата размещения материала на сайте: 17 марта 2011 года